
Zadanie Biura (biu)
Pomóż nam usprawnić bazę zadań!
Biura
Limit pamięci: 64 MB
Firma Bajtel jest potentatem na bajtockim rynku telefonów komórkowych. Każdy jej pracownik otrzymał służbowy telefon, w którym ma zapisane numery telefonów niektórych swoich współpracowników (a wszyscy ci współpracownicy mają w swoich telefonach zapisany jego numer). W związku z dynamicznym rozwojem firmy zarząd postanowił przenieść siedzibę firmy do nowych biurowców. W celu polepszenia efektywności pracy zostało postanowione, że każda para pracowników, którzy będą pracować w różnych budynkach, powinna znać (nawzajem) swoje numery telefonów, tzn. powinni oni mieć już zapisane nawzajem swoje numery w służbowych telefonach komórkowych. Równocześnie, zarząd postanowił zająć jak największą liczbę biurowców, aby zapewnić pracownikom komfort pracy. Pomóż zarządowi firmy Bajtel zaplanować liczbę biur i ich wielkości tak, aby spełnić oba te wymagania.
Zadanie
Napisz program, który:
- wyczyta ze standardowego wejścia opis, czyje numery telefonów mają zapisane w swoich telefonach komórkowych poszczególni pracownicy,
- wyznaczy maksymalną liczbę biurowców oraz ich wielkości, spełniające warunki postawione przez zarząd firmy Bajtel,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite:  oraz
oraz 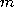 (
(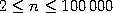 ,
,
 ), oddzielone
pojedynczym odstępem i oznaczające odpowiednio:
liczbę pracowników firmy Bajtel i liczbę par współpracowników,
którzy mają zapisane nawzajem swoje numery telefonów w swoich
telefonach komórkowych.
Pracownicy firmy są ponumerowani od
), oddzielone
pojedynczym odstępem i oznaczające odpowiednio:
liczbę pracowników firmy Bajtel i liczbę par współpracowników,
którzy mają zapisane nawzajem swoje numery telefonów w swoich
telefonach komórkowych.
Pracownicy firmy są ponumerowani od 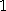 do
do  .
.
Każdy z kolejnych 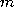 wierszy zawiera po jednej parze liczb całkowitych
wierszy zawiera po jednej parze liczb całkowitych
 i
i  (
(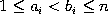 dla
dla 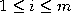 ),
oddzielonych pojedynczym odstępem i oznaczających, że pracownicy
o numerach
),
oddzielonych pojedynczym odstępem i oznaczających, że pracownicy
o numerach 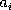 i
i 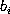 mają zapisane nawzajem swoje numery
telefonów w swoich telefonach komórkowych.
Każda para liczb oznaczających pracowników pojawi się na wejściu
co najwyżej raz.
mają zapisane nawzajem swoje numery
telefonów w swoich telefonach komórkowych.
Każda para liczb oznaczających pracowników pojawi się na wejściu
co najwyżej raz.
Wyjście
Pierwszy wiersz wyjścia powinien zawierać jedną liczbę całkowitą: maksymalną liczbę biurowców, które powinna zająć firma Bajtel. Drugi wiersz wyjścia powinien zawierać niemalejący ciąg dodatnich liczb całkowitych, pooddzielanych pojedynczymi odstępami, oznaczających wielkości biurowców (liczby rozlokowanych w nich pracowników). Jeżeli istnieje więcej niż jedno poprawne rozwiązanie, Twój program powinien wypisać dowolne z nich.
Przykład
Dla danych wejściowych:
7 16 1 3 1 4 1 5 2 3 3 4 4 5 4 7 4 6 5 6 6 7 2 4 2 7 2 5 3 5 3 7 1 7
poprawną odpowiedzią jest:
3 1 2 4
Przykładowy dobry przydział pracowników do biur wygląda następująco: do pierwszego biura pracownik o numerze 4, do drugiego pracownicy 5 i 7, a do trzeciego pracownicy 1, 2, 3 i 6.
Autorzy zadania: Marek Cygan i Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English